Abstract
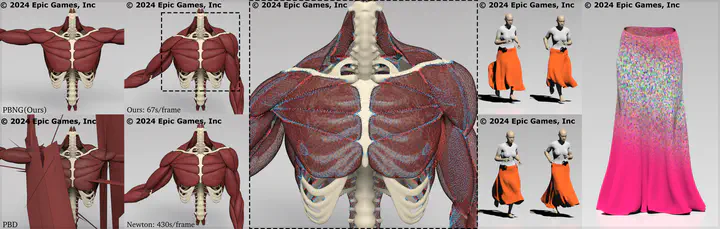
Position based dynamics is a powerful technique for simulating a variety of materials. Its primary strength is its robustness when run with limited computational budget. Even though PBD is based on the projection of static constraints, it does not work well for quasistatic problems. This is particularly relevant since the efficient creation of large data sets of plausible, but not necessarily accurate elastic equilibria is of increasing importance with the emergence of quasistatic neural networks. Recent work has shown that PBD can be related to the Gauss-Seidel approximation of a Lagrange multiplier formulation of backward Euler time stepping, where each constraint is solved/projected independently of the others in an iterative fashion. We show that a position-based, rather than constraint-based nonlinear Gauss-Seidel approach resolves a number of issues with PBD, particularly in the quasistatic setting. Our approach retains the essential PBD feature of stable behavior with constrained computational budgets, but also allows for convergent behavior with expanded budgets. We demonstrate the efficacy of our method on a variety of representative hyperelastic problems and show that both successive over relaxation (SOR), Chebyshev and multiresolution-based acceleration can be easily applied.